It is 58 B.C. and a Roman general sits atop a hill studying the opposing army, consisting of warriors from several Gallic tribes, in what is now a forested area on the eastern side of central France. He receives a message from Julius Caesar, his commander, and is quite certain no one else has read it. 

Jenny logs into her bank account using her password. She is quite certain no one else can read her account balance or uncover her account number. 

Kevin makes a purchase using his debit card and pin number. Again, he and his bank can be certain no one else is making this transaction. 

What do these three situations have in common? All three involve some sort of secret sharing scheme. The study of secret sharing is known as cryptography. In this article, I will take you on a historical journey through this fascinating subject. In a future article, I will go over more of the science of cryptography.

Caesar Shift 

One of the first recorded secret-sharing schemes is known as the Caesar Shift. The idea is to take a message and shift each letter in the text three places (or any number 1-25) forward or back in the alphabet: A→D, B→E, M→P, Z→C and then A→D again. The security is given by the key, which is how many places to shift the letters. Then anyone knowing the key can quickly read the message. 

The Caesar Shift, while neat, is not very secure. In times of less literacy, it was secure, but in modern times it falls quite quickly to frequency analysis, using the fact that all letter As get encoded by the same letter (D) each time. This results in the relative frequencies of the letters and words staying the same: E is the most common letter—which would be H in this Caesar Shift. Similarly, “a,” “an” and “the” are the most common words, which would become “d,” “dq” and “wjh.” 

Vigenère Cypher

The next step forward in cryptography was the Vigenère Cypher—chronicled first in 1553 by Giovan Battista Bellaso but then miscredited to another 16th century cryptographer Blaise de Vigenère—which uses a key word to shift the letters of the message. For example, if we pick the key word “dance,” we would obtain a shift key of 4, 1, 14, 3, 5. Given the message “meet at noon,” we would shift the first letter by 4, the second by 1, the third by 14, the fourth by 3, the fifth by 5, and then repeat: the sixth by 4 and so on. The advantage here is that two occurrences of E would be encoded differently, hence the frequency analysis would not be quite as effective. 

As is the case with the Caesar Shift, there are known attacks on the Vigenère Cypher which are very effective at breaking it. They can be done by hand with some work. 

With the Vigenère Cypher, we begin to see how mathematics was applied to early cryptography. We can replace letters with their equivalent place in the alphabet, then with the key word, this becomes a sequence of shift numbers. The next step is to add each key letter into the plain text letter. If the result is more than 26, we do “clock arithmetic” and subtract 26 to obtain a result between 1 and 26. What we mean here is the following: If we have the letter Y it corresponds to the number 25. If we then us the key letter D, corresponding to 4 we add 4 to 25 to obtain 29. The challenge is that 29 is not in our list of 1-26. So what we do is subtract 26 to obtain 3, which is then the code letter C. 

Enigma 

The mathematical nature of cryptography developed through the centuries such that cyphers become entirely mathematical by World War II, during which there were significant advancements in cryptography and cryptanalysis (the study of cryptosystems). The Germans developed an entirely new machine and encryption/decryption system called Enigma. This was no ordinary substitution cypher. Enigma relied on three wheels, each of which was a permutation cypher; a plug board, which was another permutation; and a reflector. 

When a key was pressed on the Enigma machine the letter was passed through the plugboard, then through each of the three permutation discs, hit the reflector, back through the permutation discs, then to a light board showing the encrypted letter. Then when the next key was pressed, the first wheel was rotated so that it aligned with the other two differently. Hence the entire system changed a bit. 

The Germans thought that this code was unbreakable. But three Polish mathematicians, after a few weeks of listening to German radio communication, were able to not only break the codes but build a machine similar to what the Germans had without ever seeing it. They then went on to build a machine to break the codes called the bomba kryptologiczna or cryptologic bomb.

Shortly before Poland was invaded, these three mathematicians presented their work at a conference to French and British cryptographers. Thus, they passed on their knowledge of not only how the codes worked but how to break them. Alan Turing used the information from the Polish cryptographers to develop the British Bombe, the electromechanical device used to break the enigma codes throughout the war. Many historians believe that knowing how to break the codes shortened the war by at least two years. 

The Cold War

A new era of cryptography began after World War II at the start of the Cold War. Information security was considered an absolute necessity by the U.S. and USSR. Both countries set up agencies dedicated to information security and warfare. Cryptography entered the academic research mainstream.

The U.S. developed the Data Encryption Standard (DES) for secret communications, which was deployed from 1979 to 2005. DES uses a 56-bit key (a string of 56 zeroes and ones) and works on block lengths of 64 bits. DES is considered insecure by modern standards because the encryption is easily broken.

Advanced Encryption Standard

In 2000, the Advanced Encryption Standard (AES) replaced DES. AES also works on blocks of data and can accept keys up to 256 bits in length. Currently, AES serves as the standard for encryption in the U.S. and many parts of the world. It is used heavily in internet communication because it is fast and secure. 

Security Concerns

All the codes mentioned so far are termed symmetric cyphers, meaning that both the sender and receiver need to have the same key to encrypt and decrypt messages. This poses a challenge in that some other communication method must be used to share the secret keys since the internet might not be insecure. Embassies, for example, relied on DES for decades. Diplomats used diplomatic pouches—which by international agreement, cannot be opened at border crossings—to deliver secret keys to and from their governments to their embassies and consulates. 

The underlying reason for this is a fundamental of cryptography, Kerckhoffs’s principle (after a 19th-century Dutch linguist and cryptographer) states: A cryptosystem should only depend on the key, not on the algorithm used. What this means is that a secure cryptosystem should be able to share how it works with any user, including the attacker, but should still be secure as long as the key is kept secure. Another way to say this is: “Security through obscurity is not security.” That is, all security systems should be secure even if publicly known. As a corollary to Kerckhoffs’s principle and this statement is that the more secrets a security system has, the more vulnerabilities it also possesses.

Both DES and AES are public algorithms in that how they work is completely known. This allows for any cryptographer to study the algorithm and see if flaws can be found. A fundamental rule of cryptography is that anyone can make a system that he or she can’t break, but, no matter how complex, someone else might be able to break the system. 

So, DES and AES satisfy Kerckhoff’s principle in that the only piece of information that is needed for the system to be secure is the key. 

One-Time Pad

The ultimate in security is given by the one-time pad. Here the secret key is at least as long as the message. What we want the key to be is as random as possible, in order that an eavesdropper not only can’t read the message but can’t tell that it’s a message in the first place—analogous to background noise in electric transmissions. The key is then used to encrypt the message letter by letter. The result, if the key indeed looks like noise, is a message that appears to be random noise. Any plain text of the same length as the encrypted text is just as likely. As an example, if we encode “truth” using a particular one time pad we might obtain the cypher text “AQHBT”. Now if we know the key, we easily obtain our original message. But it turns out that without the correct key, a different key could give any other five letter word, such as “whose.” As a result, the one-time pad provides the highest level of security. 

Key Exchange and Public Key Cryptography

The challenge for the one-time pad is that both sides need to have obtained the same secret key somehow. In 1976, two researchers from Stanford University, Whitfield Diffie and Martin Hellman, published a paper that revolutionized cryptography and made encryption across the internet possible. In this paper, they introduced the notion of public key cryptography. 

Public key cryptography is different than symmetric key cyphers (where the encryption and decryption keys are the same) in that there are two different keys, one for encryption and one for decryption. A user is then able to publish his or her encryption key that anyone can use to encrypt messages. The message is then decrypted using the decryption key or private key. 

While they didn’t have a public key cryptosystem, they did publish a method for two people to develop a key across an insecure channel. Using this key exchange, two users can have the same private key that an observer cannot obtain by any known method except brute force (testing all possibilities), which would take thousands of years. The two users would then use an agreed-upon symmetric algorithm like AES.

RSA

Public key cryptography became a reality with the development of a new algorithm by Rivest-Shamir-Adleman known as RSA. The math behind RSA is not terribly difficult and is accessible to an advanced high school student. However, without the secret numbers—two secret numbers (prime numbers of 200 digits or more) are chosen to generate the private key—it is very difficult to generate the private key from the public key, unless one has thousands of years of computer time available.

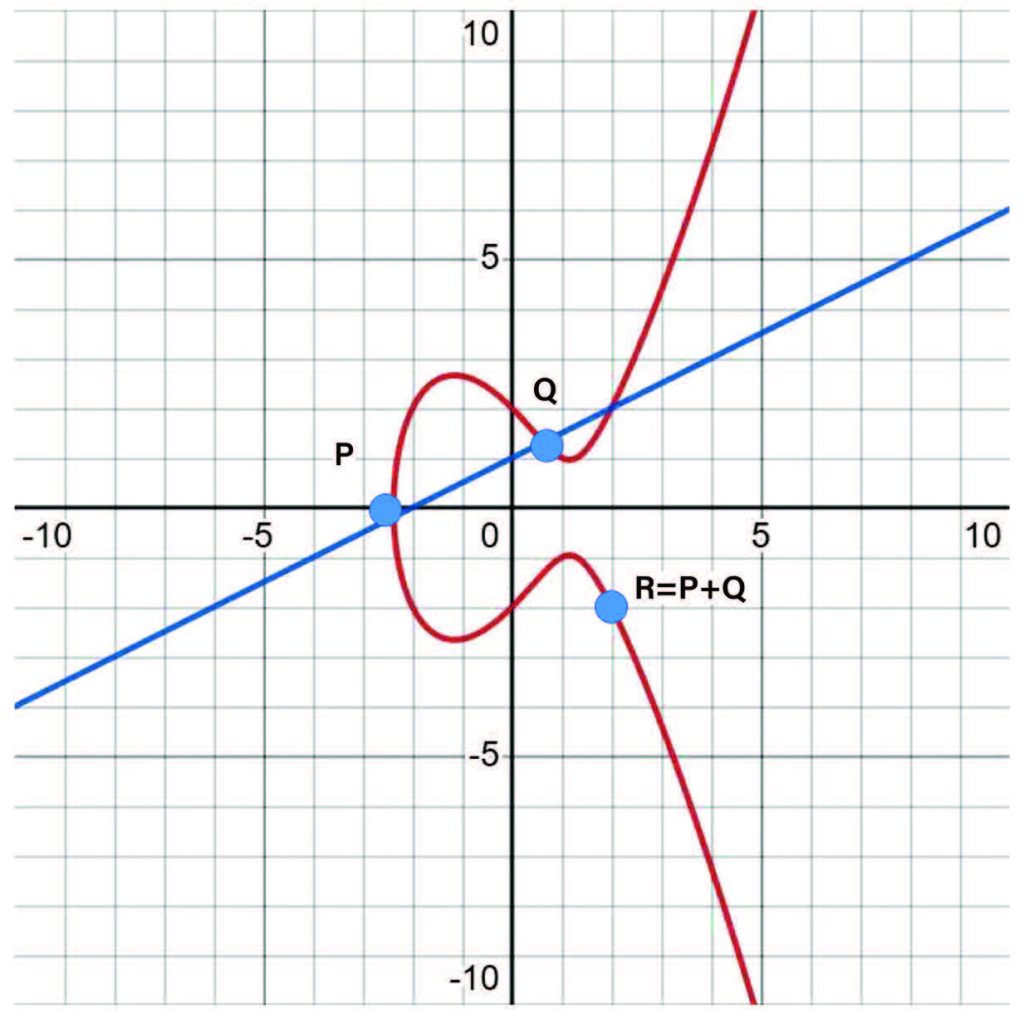
Elliptic Curve Cryptography

The next major advancement in public key cryptography came in the form of elliptic curves (y2=x3+ax+b). In the xy-plane, shown in the graph below, elliptical curves are well behaved, but in clock arithmetic they act somewhat randomly, which makes them quite adept at generating secret keys. Using surprisingly simple math equations, we can produce these common secret keys. This key-exchange algorithm has become the standard at many websites, including Google and Wikipedia. 

The magic of elliptic curve cryptography is that the key size is significantly shorter than the RSA keys. As a comparison, an elliptic curve key of length 256 bits is equivalent to an RSA key of 4096 bits. Further, the algorithm is very fast.

Digital Signatures 

One fascinating facet of all current public key algorithms is that the public key and private key can be applied in any order. This allows for signing of documents. What the user does is apply his or her private key to the document to “sign” it. Anyone can then verify the signature by applying the appropriate public key. Two users can sign the same document by applying their private keys in succession. Then again, the signatures can be verified by applying the appropriate public keys. 

Bitcoin

The bitcoin algorithm uses elliptic curve cryptography in its implementation. What bitcoin is at its core is a ledger of how much bitcoin an account has. The accounts are given by public keys of the elliptic curve cryptosystem. When a user wants to spend their Bitcoin, they specify a different account and then sign the transaction with their private key. Anyone can verify this is a legitimate transaction by applying the public key to the transaction. There is more that goes into the algorithm, but this is the heart of how transactions work. 

Protection vs Security & Privacy 

The American public is heavily reliant on cryptography for day-to-day functions. From securely browsing the internet, to chip-and-pin transactions on debit cards, or chip-only transactions with credit cards. Further, there are many chat programs that rely on cryptography to keep the user’s messages secure from eavesdroppers.

Currently, however, there is legislation under consideration in Congress, which according to many experts unintentionally puts digital privacy at risk for private citizens and the business and industry sectors. 

The EARN IT Act was originally introduced in 2020 with the aim of protecting children from online sexual exploitation. Strong public opposition and pushback from human rights organizations caused the bill to be shelved. Then the bill was re-introduced to the U.S. Senate in February 2022 and soon endorsed by the National Center for Missing and Exploited Children and the National Center on Sexual Exploitation. The bill would create a National Commission on Online Child Sexual Exploitation Prevention with laudable goals. 

The problem is that implementation would almost certainly grant the government access to end-to-end encryption in order to identify, track and prosecute criminals. End-to-end encryption is fundamental to privacy for email providers and security for business communications, which often involve highly sensitive data. Legislating backdoors to this encryption will allow access without notification not only to government agencies, including law enforcement, at the local, state and federal levels—but worse, the backdoors will also enable hackers to gain the same access.

In short, privacy and security in digital services and communications will be irreparably shattered. Not surprisingly, the government will be exempt from these measures. The Electronic Frontier Foundation criticized the EARN IT Act as “a direct threat to constitutional protections for free speech and expression.” In a poll this July from AXIS Research, respondents identified privacy (21 percent) as the top issue Congress should focus on concerning tech-related issues. Protecting children online certainly concerns voters but ranked third at 11 percent.

The choice between privacy and protection, unfortunately, is a fundamental either/or. There is no legislative fence to land on; encryption’s backdoor is open or shut, never slightly ajar. 

Further Reading

If you are interested in learning more about cryptography, there are a few excellent texts available:

Serious Cryptography by Jean-Philippe Aumasson is accessible to many but has some technical details.

For those more interested in the algorithms, I recommend the classical text Applied Cryptography by Bruce Schneier.

The mathematics behind the algorithms is discussed in Introduction to Cryptography with Coding Theory by Wade Trappe and Lawrence Washington.

For more information on Kerckhoffs’s principle, see this article: https://www.schneier.com/crypto-gram/archives/2002/0515.html#1

Lastly, I will be teaching a course on cryptography through the Dakota Digital Academy and Dickinson State University in the spring of 2023.